نمایش ژنوتیپ Genotype

نمایش ژنوتیپ Genotype

یکی از مهمترین تصمیم گیری ها در هنگام اجرای یک الگوریتم ژنتیک ، تصمیم در خصوص نحوه نمایشی است که برای نشان دادن راه حل مسائله از آن استفاده می کنیم. دلیل اهمیت هم آن است که نمایش نامنساب می‌تواند منجر به کارایی پایین الگوریتم ژنتیک گردد.بنابراین نمایش انتخاب نحوه نمایش مناسب ،تعریف مناسبی از نگاشت میان فضاهای ژنوتیپ و فنوتیپ را شامل می‌شود و از ملزومات موفقیت الگوریتم ژنتیک می باشد.در این بخش  تعدادی از پرکاربردترین شیوه‌های نمایش الگوریتم های ژنتیک را نشان می دهیم.هر چند نحوه نمایش یکی از مسائل بسیار سخت است شخص ممکن است که نیاز به نحوه های نمایش دیگر داشته باشد و یا ترکیبی از نحوه های نمایشی را که توضیح داده خواهد شد را برای مطابقت با مسائله خود به کار گیرد.

نمایش دودویی :
نمایش دودویی یکی از ساده‌ترین و پر استفاده ترین شیوه‌های نمایش در الگوریتم های ژنتیک است.دراین نوع از نمایش ژنوتیپ شامل رشته ای از بیت‌ها می باشد.برای بعضی از مسائل  زمانی که راه حل شامل متغیرهای تصمیم گیری بولین (yes/no ) می‌باشد نمایش به صورت باینری (دودویی) امری طبیعی است.برای مثال در مسائله کوله پشتی 1/0 (0/1 Knapsack Problem) .اگر n آیتم وجود داشته باشد ، می‌توانیم راه حل را بوسیله یک رشته دودویی از n عنصر نمایش بدهیم ، بطوری که X امین عنصر (x ^th) می‌گوید که آیتم x برداشته شده است (۱) یا خیر (0)

برای مسائل دیگر بویژه مسائلی که با اعداد سر و کار دارند ، می‌توانیم اعداد را به صورت حالت دودویی آن‌ها نشان بدهیم.مشکل با این نوع از رمزگذاری (encoding  ) این است که بیتهای مختلف دارای اهمیت متفاوتی هستند ، بنابراین عملگرهایی مثال جهش (mutation) و متقاطع (crossover ) می‌توانند اثرات ناملطوبی داشته باشند.این مشکل می‌تواند تا حدی با استفاده از Gray Coding حل شود ، بدین صورت تغیر در یک بیت تأثیرات خیلی زیادی در حل مسائله نخواهد داشت.

نمایش مقدار دهی واقعی (Real Valued Representation):
برای مسائلی که می‌خواهیم ژنها را با استفاده از متغیر های متوالی بجای متغیر های گسسته تغریف کنیم ، نمایش مقدار دهی واقعی طبیعی ترین روش است.اگر چه دقت این مقدار دهی واقعی یا نقطه اعشار اعداد یکی از محدودیت‌ها برای کامپیوتر است.در این روش نمایش مقدار هر چیزی مرتبط با مسائله می‌تواند باشد.و هر کروموزم می‌تواند شامل یک مقدار باشد.

نمایش صحیح (Integer Representation)

برای ژنهایی با مقادیر گسسته ، همیشه نمی‌توانیم راه حل را به فضای دودویی yes یا no محدود نماییم.برای مثال اگر با می‌خواهیم چهار مسیر شمال ، جنوب ،شرق و غرب را رمزگذاری کنیم، می‌توانیم آن‌ها را به صورت {۰،۱،۲،۳} رمز گذاری نماییم.در چنین مواردی نمایش صحیحی مورد استفاده است.

نمایش جایگشتی :

در اکثر مسائل ،راه حل بوسیله ترتیبی از عناصر نمایش داده می شود.در این‌گونه موارد جایگشت یکی از بهترین روش‌های نمایش است.یک مثال کلاسیک از این نحوه نمایش مسائله فروشنده دوره‌گرد (travelling salesman problem (TSP)) است.در مسائله فروشنده یک سفر به همه شهر ها خواهد داشت، هر شهر را دقیقاً یک بار بازدید نموده و به شهری که سفر را از آن شروع نموده است باز می گردد.جمع طول کل مسیر طی شده برای این سفر باید کمترین باشد.راه حل مسائله فروشنده دوره‌گرد به صورت طبیعی ترتیبی یا جایگشتی از همه شهرهاست و بنابراین استفاده از نمایش جایگشتی برای این مسائله مناسب به نظر می رسد.در واقع هر کروموزم رشته ای از اعداد است که یک موقعیت را در یک دنباله نمایش می دهد

اصول و تعاریف اولیه الگوریتم های ژنتیک

اصول الگوریتم های ژنتیک
در این قسمت واژگان پایه  که برای فهم الگوریتم های ژنتیک مورد نیاز است را معرفی می کنیم.همچنین ساختار عمومی الگوریتم های ژنتیک هم در شبکه کد و هم به شکل گرافیکی نمایش داده می شود.به خواننده توصیه می‌شود که بطور صحیح همه مفاهیم معرفی شده در این بخش را  متوجه شده و همه آن‌ها را به ذهن بسپارید .

واژگان پایه :

قبل از اینکه شروع به بحث در خصوص الگوریتم های ژنتیک نماییم ، ضروری است که با برخی از واژگان پایه و اساسی که در کل بحث الگوریتم های ژنتیک مورد استفاده قرار می‌گیرد آشنا شویم.

• جمعیت :(Population): یک زیر مجموعه از همه راه حل‌های ( رمز شده) ممکن برای مسائله مورد مطالعه.جمعیت برای یک الگوریتم ژنتیک مشابه با جمعیت برای انسان است بجز اینکه بجای وجود  انسان ها ما راه حل‌های کاندید را داریم که وجود بشر را نشان می دهند.

• کروموزوم ها (Chromosomes) یک کروموزوم یک راه حل برای مسائله مورد مطالعه است.

• ژن :(Gene) ژن موقعیت عنصری از یک کروموزم است

• آلل (Allele) : مقداری که یک ژن برای یک کروموزم خاص دریافت می‌کند.

• ژنوتیپ(Genotype) : ژنوتیپ یک جمعیت در فضای محاسبات است.در فضای محاسبات ، راه حل‌ها به شیوه ای که به راحتی قابل فهم و مدیریت بوسیله یک سیستم محاسباتی باشند نمایش داده می‌شوند.

• فنوتیپ (Phenotype) :فنوتیپ  جمعیتی در فضای راه حل یک  دنیای واقعی موجود می‌باشد که در آن راه حل‌ها به شیوه ای نمایش داده می‌شوند که آن‌ها در موقعیت های دنیای واقعی نمایش داده شده‌اند.

• رمز گشایی و رمز گذاری (Decoding and Encoding) : در مسائل ساده فضای  فنوتیپ و ژنتیپ مشابه هستند.اگرچه در اغلب موارد  فضای  فنوتیپ و ژنتیپ با یکدیگر متفاوت هستند.رمز گشایی فرآیند انتقال یک راه حل از فضای ژنوتیپ به فضای فنوتیپ، در حالی که رمزگذاری فرآیند  انتقال از فضای فنوتیپ به ژنوتیپ می‌باشد.رمزگذاری باید به قدر کافی سریع باشد این فرآیند مکرراً در خلال محاسبه مقدار fitness (سازگاری) انجاممی‌شود.

برای مثال در مسائله کوله پشتی 0/1 (0/1 Knapsack Problem).فضای فنوتیپ شامل راه حل‌هایی است که فقط شامل تعداد آیتم هایی است که از آیتم های موجد برداشته شده اند برداشته شده‌اند.به هر حال ، در فضای ژنوتیپ مثال ذکر شده در بالا می‌تواند به عنوان یک رشته دودویی با طول n نمایش داده شود ( که در اینجا n تعداد آیتم هاست). صفر (۰) در موقعیت x نمایش می‌دهد که x امین (x th) آیتم برداشته شده است در حالیکه وجود 1 برعکس آن را نشان می دهد( x امین آیتم برداشته نشده است).این نمونه‌ای است که در آن فضای ژنوتیپ و فنوتیپ با یکدیگری متفاوت هستند.

• تابع سازگاری (Fitness Function ) : یک تعریف ساده از  تابع سازگاری تابعی است که راه حل را به عنوان ورودی دریافت می نماید و راه حل مناسب را به عنوان خروجی تولید می‌کند.در بعضی از موارد ، تابع سازگاری و تابع هدف یکسان هستند و در بعضی دیگر بر اساس مسائله ممکن است که متفاوت باشند.

• عملگر ژنتیکی(Genetic Operators ) : عملگرهای ژنتیکی ترکیب ژنتیکی فرزندان را تغییر می‌دهند .برای مثال می‌توان به عملگر های انتخاب(selection) ، جهش(mutation)  ،متقاطع (crossover)و غیره نام برد.

ساختار پایه الگوریتم های ژنتیک
ساختار پایه یک الگوریتم ژنتیک به شرح ذیل است :
از یک جمعیت اولیه شروع می‌کنیم ( که می‌تواند به صورت تصادفی یا شیوه‌های ابتکاری دیگر تولید شده باشد) .والدینی را از این جمعیت برای زاد و ولد انتخاب می‌کنیم.عملگرهای crossover و mutation (جهش) را روی والدین برای تولید نمودن فرزندان جدید اعمال می‌کنیم و سرانجام این فرزندان اشخاص موجود را در جمعیت جایگزین نموده و فرآیند تکرار می‌شود. در این روش الگوریتم های ژنتیک سعی می‌کنند تا شیوه تکامل بشری را تا حدی تقلید کند.

و در انتها شبه کدی که یک الگوریتم ژنتیک را شرح می‌دهد در زیر آورده شده است

GA()
   initialize population
   find fitness of population
   
   while (termination criteria is reached) do
      parent selection
      crossover with probability pc
      mutation with probability pm
      decode and fitness calculation
      survivor selection
      find best
   return best

مقدمه‌ای بر الگوریتم های ژنتیک

مقدمه‌ای بر الگوریتم های ژنتیک :
الگوریتم ژنتیک (Genetic Algorithm -GA) یک تکنیک بهینه سازی بر اساس جستجو می‌باشد که بر اصول ژنتیک و انتخاب طبیعی(Natural Selection) پایه گذاری شده است.این تکنیک به کرات برای یافتن راه حل بهینه یا نزدیک به بهینه مورد استفاده قرار می‌گیرد تا بدین وسیله مسائل مشکلی که ممکن است توسط روشهای دیگر در زمان طولانی حل شوند را در یک زمان مناسب و بهینه حل نماید.اغلب اوقات از این تکنیک در پژوهش ها و یادگیری ماشین برای حل مسائل بهینه سازی (optimization problems مسائلی که در آن بهترین راه حل از میان همه راه حل‌های ممکن یافت می شود)استفاده می‌شود
مقدمه ای بر بهینه سازی :

بهینه سازی پروسه‌ ساخت یک چیز بهتر است.در هر پروسه ، یک مجموعه از ورودی ها داریم و یک مجموعه از خروجی ها که در شکل زیر نشان داده شده‌اند

بهینه سازی به پیدا کردن مقادیری از ورودی ها اطلاق می‌شود به نحوی که بهترین مقادیر خروجی را بدست بیاوریم. تعریف بهترین از مسائله به مسائله دیگر متفاوت است اما در اصطلاح ریاضیات به حداکثر رساند یا به حداقل رساندن یک یا چند تابع هدف از طریق تغییر دادن پارامتر های ورودی اطلاق می‌شود.یک مجموعه از همه راه حل‌های ممکن یا مقادیر ورودی می‌تواند فضای جستجو را تکشیل دهد.در این فضای جستجو یک نقطه یا یک مجموعه از نقاط که راه حل بهینه را فراهم می‌کنند پنهان شده‌اند. وظیفه نهایی بهینه سازی پیدا کردن نقطه یا مجموعه‌ای از نقاط در فضای جستجو است.
الگوریتم های ژنتیک چه هستند ؟
طبیعت همیشه یک منبع بزرگ از الهام برای همه نسل بشر بوده است.الگوریتم های ژنتیک الگوریتم هایی بر اساس جستجو هستند که بر پایه مفهوم انتخاب طبیعی و ژنتیک پایه گذاری شده است.الگوریتم های ژنتیک زیر مجموعه‌ای از یک شاخه بسیار بزرگ‌تر از محاسبات که معروف به محاسبات تکاملی (Evolutionary Computation) است می‌باشند.الگوریتم های ژنتیک بوسیله John Holان وی در دانشگاه میشیگان توسعه داده شد و از این الگوریتم ها برای حل مسائل مختلف بهینه سازی با درجه بالایی از موفقیت استفاده شده است.
در الگوریتم های ژنتیک یک مخزن یا مجموعه از راه حل‌های ممکن برای مسائله داده شده داریم.این راه حل‌ها تحت عملیات های نوترکیبی (recombination) و جهش(mutation) شبیه آنچه در ژنتیک طبیعی رخ می‌دهد ، فرزندان جدیدی تولید می‌کنند.این پروسه در نسل های مختلف تکرار می‌شود.به هر فرد ( یا راه حل کاندید) یک مقدار متناسب اختصاص داده می شود( بر اساس مقدار تابع هدف آن) و افراد شاخص شانس بالاتری برای زاد و ولد و تولید افراد شاخص تر دارند. این در‌واقع تعریف تئوری داروین است که معتقد به بقای نسل اصلحتر می‌باشد.در این روش بهترین افراد یا راه حل‌ها در نسل های ایجاد شده استخراج می‌شوند.این کار تا رسیدن به یک معیار توقف ادامه می‌یابد.الگوریتم های ژنتیک به اندازه کافی در طبیعت تصادفی هستند، اما آن‌ها عمل‌کرد خیلی بهتری از جستجوی محلی تصادفی دارند( که در آن ما فقط راه حل‌های تصادفی مختلف را مورد برآورد قرار می‌دهیم).

مزایای الگوریتم های ژنتیک :
الگوریتم های ژنتیک دارای مزیت‌های متعددی هستند که آن‌ها را فوق‌العاده محبوب و مورد استفاده نموده است

•     نیاز به هیچ اطلاعات فرعی ( مشتق شده) نیست .که ممکن است برای اغلب مسائل دنیای واقعی در دسترس نباشد.
•     قابلیت‌های بسیار خوب برای موازی سازی دارد
•     هر دو تابع های گسسته و پیوسته را بهینه سازی می نماید و همچنین مسائل چند هدفه را ( multi-objective)0
•     لیستی از راه حل‌های خوب را بجای یک راه حل یکتا تهیه می‌کنند
•     همیشه یک راه حل برای مسائل دارند در طول زمان بهتر می‌شود
•     هنگامی که فضای جستجو بسیار بزرگ است و تعداد زیادی از پارامتر ها در مسائله درگیر هستند مفید هستند

محدودیت‌های الگوریتم های ژنتیک :
شبیه هر تکنیک دیگری الگوریتم های ژنتیک از یکسری محدودیت‌ها رنج می‌برند که شامل موارد زیر است :

•     الگوریتم های ژنتیک برای همه مسائل مناسب نیستند مخصوصاً آن دسته از مسائلی که ساده هستند و اطلاعات مشتق شده (derivative information) برای آن‌ها موجود باشد
•     مقدار متناسب ( مناسب) مکرراً محاسبه می‌شود که ممکن است برای بعضی از مسائل محاسباتی پر هزینه و گران باشد
•     تصادفی بودن باعث می‌شود که هیچ تضمینی برای بهینه بودن یا کیفیت راه حل وجود نداشته باشد
•     اگر درست اجرا نشود الگوریتم ژنتیک ممکن است که یک راه حل بهینه را بوجود نیاورد.

انگیزه برای استفاده از الگوریتم های ژنتیک :
الگوریتم های ژنتیک این توان را دارند که راه حل‌هایی به اندازه کافی سریع و به اندازه کافی خوب فراهم کنند.این ویژگی‌ها باعث می‌شود که الگوریتم های ژنتیک برای استفاده در حل مسائل مربوط به بهینه سازی جذاب باشند.دلایلی مورد نیاز بودن الگوریتم های ژنتیک به شرح ذیل می‌باشد :
حل مسائل مشکل
در علوم کامپیوتری ، مجموعه‌ای از مسائل موجود است که در دسته NP-Hard قرار می گیرند.و این بدان معناست که حتی قوی‌ترین سیستم‌های محاسبه ای برای حل این مسائل نیازی صرف زمان خیلی طلانی دارند ( حتی سالها).در چنین سناریوهایی یک ابزار ثابت شده و خوب برای فراهم نمودن یک راه حل نزدیک به بهینه در یک مدت زمان کوتاه است.
شکست روش‌های مبتنی بر گرادیان.
روش‌های محاسبه قدیمی با شروع در یک نقطه تصادفی و حرکت در یک جهت از گرادیان تا رسید به بالاترین مکان کار می کنند.این تکنیک برای توابع هدفی که تنها یک نقطه اوج دارند مثل تابع هزینه در رگرسیون خطی.اما در اغلط موقعیت های دنیای واقعی با مسائل خیلی پیچیده‌ای سر و کار داریم که به landscapes (منظره ها) معروف هستند ، که از تعدادی زیادی قله و دره ساخته شده اند.که باعث می‌شوند متد های قدیمی که شرح داده شده در مواجه با آن موفق نباشند. این متدها از گرایش ذاتی به گیر افتادن در نقطه قله مطلوب محلی رنج می برند.این مطلب در شکل زیر نمایش داده شده است :


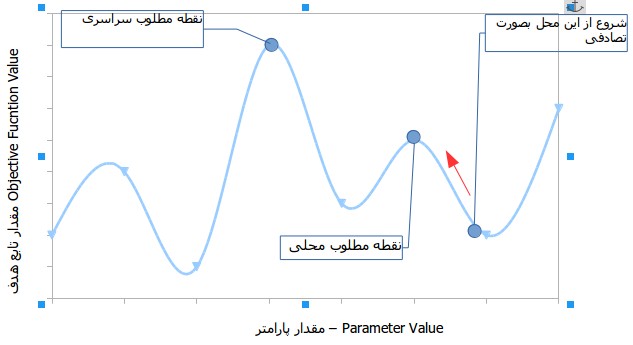
بدست آوردن راه حل خوب با سرعت مناسب
برخی از مسائل مشکل مثل مسائله فروشنده دوره‌گرد (Travelling Salesperson Problem -TSP) دارای کاربرد در دنیای واقعی هستند.مثل پیدا کردن مسیر و طراحی VLSI .حالا فرض کنید که شما از سیستم ناوبری GPS استفاده می‌کنید و برای محاسبه مسیر بهینه از مبداء به مقصد چند دقیقه ( یا حتی چند ساعت) صرف می‌کنید . تأخیر در اینگونه برنامه‌های کاربردی در دنیای واقعی پذیرفتی نیست پس ش یک راه حل به اندازه کافی خوب راه حلی است که به اندازه کافی هم سریع باشد