استفاده از الگوریتم ژنتیک برای حل یک معادله ساده ریاضی

استفاده از الگوریتم ژنتیک برای حل یک معادله ساده ریاضی
این مطلب استفاده از الگوریتم ژنتیک را به شکلی ساده به همراه مثال برای افراد مبتدی شرح می دهد.ابتدا فلسفه اساسی و فلوچارت این الگوریتم شرح داده می شود و در مرحله بعد محاسبات قدم به قدم الگوریتم ژنتیک برای حل یک مسائله ساده تساوی ریاضیات بصورت کامل شرح داده می شود.
فلسفه پایه الگوریتم های ژنتیک
الگوریتم ژنتیک بوسیله goldberg توسعه و گسترش یافت که الهام گرفته  از تئوری تکامل داروین است ، مبنای این نظریه هم بقای گونه ها بر اساس میزان ارزش انها ست هرچه قوی تر احتمل بقا هم بیشتر. .داروین همچنین معتقد است که بقای یک نسل می‌تواند بوسیله فرآیند تولید مثل انتخاب ، برش و جهش  حفظ شود. بعدها از ایده داروین در خصوص تکامل برای بدست آوردن راه حل بهینه در مسائل محاسباتی استفاده شد که یکی از معروف ترین این الگوریتم ها ، الگوریتم ژنتیک است.

راه حلی که توسط الگوریتم های ژنتیک تولید می‌شود یک کروموزوم نامیده می‌شود و  مجموعه از کروموزم ها ، جمعیت population نامیده می شوند.کروموزم ها از ژنها تشکیل شده‌اند و مقدار آن می‌تواند عددی ، دودویی ، سمبل ها یا کاراکتر ها باشد که وابسته به مسائله است که قصد حل نمودن آن را داریم.شایان ذکر است نحوه نمایش کروموزوم ها و مقادیر ژنها یکی از اساسی ترین  قسمت های حل یک مسائله با استفاده از الگوریتم ژنتیک است و دیگر قسمت بسیار مهم در این الگوریتم ها تعریف تابع برازش است که در قسمت بعدی به ٔآن پرداخته می شود.
ارزش و بهای هر کروموزم توسط تابعی تحت نام برازش اندازه گیری می شود ، در واقع تابع برازش میزان مفید و مناسب بودن راه حل برای مسائله مورد نظر را اندزه گیری می نماید.پس ‌از هر مرحله ای که الگوریتم ژنتیک تکرار شد برازش هر یک از راه حل های تولید شده ( کروموزوم ها ) اندزه گیری می شود.برخی از کروموزم ها درون جمعیت تحت پروسه‌ای به نام crossover با یکدیگر ترکیب می‌شوند و بدین صورت کروموزم های جدیدی که فرزند نامیده می‌شود تولید می‌کنند که ترکیب ژن این کروموزم های جدید ترکیبی از ژنهای والدین آنهاست.در یک نسل تعدای از کروموزومها نیز در ژنهای خود دچار جهش mutation می شوند.
تعداد کروموزوم هایی که تحث تأثیر crossover و جهش mutation قرار میگیرند بوسیله نرخ برش و نرخ جهش کنترل می شوند.کروموزومی در جمعیت که برای نسل بعدی حفظ و نگاهداری می‌شود بوسیله قانون تکامل داروین انتخاب می شود.کروموزمی که مقدار برازش بالاتری دارد از احتمال بالاتری برای انتخاب دوباره در نسل بعدی برخوردار است.بعد از چندین نسل ، مقدار کروموزم به یک مقدار خاص که بهترین راه حل برای مسائله است همگرا می شود.
مراحل الگوریتم ژنتیک
۱: در الگوریتم ژنتیک فرآیند به شرح ذیل است
قدم ۱ : تعداد کروموزوم ها ، نسل ها و نرخ جهش و نرخ برش  معیین می شود
قدم ۲: بر اساس تعداد جمعیت کروموزوم – کروموزوم   ایجاد می شود و ژنهای کروموزوم –   با یک مقدار تصادفی مقدار دهی اولیه می شوند.
قدم ۳ : قدم‌های ۴-۷ را تا زمانی که تعداد نسل ها برآورده شود ( تأمین شود) انجام می شود
قدم ۴ :مقدار برازش کروموزوم  بوسیله محاسبه تابع هدف objective function مورد ارزیابی قرار می گیرد
قدم ۵ : انتخاب کرموزوم
قدم ۵ : برش
قدم ۶:جهش
قدم ۷: کرموزم جدید (فرزند)
قدم ۸ :راه حل( بهترین کرموزوم ها)
فلوچارت الگوریتم را می‌توان در شکل زیر مشاهده نمود :

مثال عددی
در اینجا یک مثال از کاربردی که از الگوریتم ژنتیک برای حل نمودن یک مسائله ترکیبی استفاده می‌کند را توضیح می دهیم.فرض کنیم که تساوی زیر را داریم
a+db+3c+4d=30
از الگوریتم ژنتیک برای بدست آوردن مقادیر a,b,c,d تا برای حل تساوی ذکر شده استفاده می کنیم.
.در ابتدا باید تابع هدف را فرمول کنیم ، برای این مسائله هدف مینیمم نمودن مقدار تابع f(x)  جایی که
 f (x) = ((a + 2b + 3c + 4d) – 30)
از آنجا که چهار متغیر در تساوی وجود دارد ، یعنی a,b,c,d می‌توانیم کروموزوم ها را به صورت زیر شکل دهیم

d

c

b

a

برای افزودن سرعت محاسبات ، می‌توانیم مقدار متغیر ها a,b,c,d را به اعداد صحیح بین ۰ تا ۳۰ محدود نماییم.
قدم اول: مقدار دهی اولیه
برای نمونه تعداد کروموزوم ها درون جمعیت را ۶ عدد تعریف می‌کنیم ، سپس مقادیر تصادفی را برای ژنهای a,b,c و d که تشکیل‌دهنده کروموزم مورد نظر ما هستند تولید می کنیم.پس همانطور که ملاحظه می شود ۶ کروموزمی را که در اختیار داریم به صورت زیر با اعداد تصادفی مقدار دهی می نماییم

Chromosome[1] = [a;b;c;d] = [12;05;23;08]

Chromosome[2] = [a;b;c;d] = [02;21;18;03]
Chromosome[3] = [a;b;c;d] = [10;04;13;14]
Chromosome[4] = [a;b;c;d] = [20;01;10;06]
Chromosome[5] = [a;b;c;d] = [01;04;13;19]
Chromosome[6] = [a;b;c;d] = [20;05;17;01]

قدم دوم : ارزیابی راه حل ها ( کروموزوم ها)

در این مرحله مقدار تابع هدف برای هر کروموزمی که در مرحله مقدار دهی جمعیت اولیه تولید شده است محسابه می شود

F_obj[1] = Abs(( 12 + 2*05 + 3*23 + 4*08 ) - 30)= Abs((12 + 10 + 69 + 32 ) - 30)= Abs(123 - 30)= 93

F_obj[2] = Abs((02 + 2*21 + 3*18 + 4*03) - 30)= Abs((02 + 42 + 54 + 12) - 30)= Abs(110 - 30)= 80
F_obj[3] = Abs((10 + 2*04 + 3*13 + 4*14) - 30)= Abs((10 + 08 + 39 + 56) - 30)= Abs(113 - 30)= 83
F_obj[4] = Abs((20 + 2*01 + 3*10 + 4*06) - 30)= Abs((20 + 02 + 30 + 24) - 30)= Abs(76 - 30)= 46
F_obj[5] = Abs((01 + 2*04 + 3*13 + 4*19) - 30)= Abs((01 + 08 + 39 + 76) - 30)= Abs(124 - 30)= 94
F_obj[6] = Abs((20 + 2*05 + 3*17 + 4*01) - 30)= Abs((20 + 10 + 51 + 04) - 30)= Abs(85 - 30)= 55

مرحله سوم : انتخاب

با ارزشترین کروموزوم از شانس و احتمال بیشتری برای برای انتخاب شدن به منظور تولید نسل بعدی دارد.برای محاسبه احتمال برازش باید برازش هر کروموزم محاسبه شود. برای جلوگیری از مشکل تقسیم بر صفر مقدار تابع هدفی که برای هر کرموزم در مرحله قبل بدست آمد با عدد ۱ جمع می شود :

Fitness[1] = 1 / (1+F_obj[1])= 1 / 94= 0.0106

Fitness[2] = 1 / (1+F_obj[2])= 1 / 81= 0.0123
Fitness[3] = 1 / (1+F_obj[3])= 1 / 84= 0.0119
Fitness[4] = 1 / (1+F_obj[4])= 1 / 47= 0.0213
Fitness[5] = 1 / (1+F_obj[5])= 1 / 95= 0.0105
Fitness[6] = 1 / (1+F_obj[6])= 1 / 56= 0.0179
Total = 0.0106 + 0.0123 + 0.0119 + 0.0213 + 0.0105 + 0.0179= 0.0845

احتمال مربوط به هر کروموزم را بو سیله فرمول P[i] = Fitness[i] / Total محاسبه می نماییم :

P[1] = 0.0106 / 0.0845= 0.1254
P[2] = 0.0123 / 0.0845= 0.1456
P[3] = 0.0119 / 0.0845= 0.1408P
[4] = 0.0213 / 0.0845= 0.2521
P[5] = 0.0105 / 0.0845= 0.1243P
[6] = 0.0179 / 0.0845= 0.2118

با توجه به احتمالاتی که در بالا محاسبه شده است مشاهده می وشد که کروموزوم ۴ بیشترین برازش را دارا می باشد و بنابراین احتمال انتخاب شدن آن برای نسل بعدی کروموزوم ها بسیار بالاست.برای فرآیند انتخاب از روش چرخ رولت استفاده می کنیم که بدین منظور ابتدا باید مقادیر احتمال تجمعی ( cumulative probability) را محاسبه کنیم:

C[1] = 0.1254

C[2] = 0.1254 + 0.1456= 0.2710
C[3] = 0.1254 + 0.1456 + 0.1408= 0.4118
C[4] = 0.1254 + 0.1456 + 0.1408 + 0.2521= 0.6639
C[5] = 0.1254 + 0.1456 + 0.1408 + 0.2521 + 0.1243= 0.7882
C[6] = 0.1254 + 0.1456 + 0.1408 + 0.2521 + 0.1243 + 0.2118= 1.0

با داشتن مقادیر احتمال تجمعی استفاده از چرخ رولت در فرآیند انتخاب امکان پذیر می گردد.فرآیند بعدی تولید یک عدد تصادفی در محدوده ۰ تا ۱ است که آن را R نامیم :

R[1] = 0.201, R[2] = 0.284, R[3] = 0.099, R[4] = 0.822, R[5] = 0.398, R[6] = 0.501
اگر برای مثال عدد تصادفی R[1]  بزرگتر از C[1] و کوچکتر از C[2] بود در این صورت     Chromosome [2] به عنوان یک کروموزوم در جمعیت جدید برای تولید نسل بعدی مورد استفاده قرار می گیرد. با توجه به مقادیر نمونه های بالا  خواهیم داشت :

NewChromosome[1] = Chromosome[2]

NewChromosome[2] = Chromosome[3]
NewChromosome[3] = Chromosome[1]
NewChromosome[4] = Chromosome[6]
NewChromosome[5] = Chromosome[3]
NewChromosome[6] = Chromosome[4]

و کروموزوم ها در جمعیت به صورت زیر خواهند شد :

Chromosome[1] = [02;21;18;03]

Chromosome[2] = [10;04;13;14]
Chromosome[3] = [12;05;23;08]
Chromosome[4] = [20;05;17;01]
Chromosome[5] = [10;04;13;14]
Chromosome[6] = [20;01;10;06]

مرحله ۴ : برش (Crossover)

در این مثال از برش یک نقطه ای(one cut point) استفاده می نماییم.به صورت تصادفی یک محل در کروموزم والدین انتخاب شده و سپس زیر کرموزوم هایی که از این نقطه بدست آمده اند در دو واحد تعویض می شود.کروموزم های والدینی که با همدیگر جفت شده اند به صورت تصادفی انتخاب می شوند و تعداد کروموزوم هایی که جفت می شوند توسط پارامتری به نام نرخ برش (Crossover rate ρc ) معین می شود.شبه کد فرآیند برش در ذیل آورده شده است :

begin

k← 0;
while(k<population) do
          R[k] ← random(0-1);
        if (R[k] < ρc ) then
                 select Chromosome[k] as parent;
         end;
          k = k + 1;
end;
end;

اگر  R [k] <ρc باشد کروموزوم K به عنوان یکی از والدین انتخاب می شود.فرض کنیم که نرخ برش را ۲۵٪ در نظر گرفته باشیم ، در این صورت کروموزم شماره k در صورتی

برای برش انتخاب می شود اگر مقدار عدد تصادفی تولید شده برای کروموزوم k کمتر از ۰.۲۵ باشد. فرآیند  را به صورت زیر ادامه می دهیم.ابتدا به تعداد جمعیتی که داریم عدد تصادفی R را تولید می نماییم:

R[1] = 0.191, R[2] = 0.259, R[3] = 0.760, R[4] = 0.006, R[5] = 0.159, R[6] = 0.340

با توجه به اعداد نمونه تصادفی که در بالا آورده شده است ، والدین  Chromosome [1], Chromosome [4] و Chromosome [5] برای عملگرد برش انتخاب می شوند.حالا با توجه این والدین ترکیب همه آنها را بدست می آوریم که بصورت زیر خواهد بود

Chromosome[1] >< Chromosome[4]

Chromosome[4] >< Chromosome[5]

Chromosome[5] >< Chromosome[1]

بعد از اتمام انتخاب کروموزوم ها برای برش ، فرآیند بعدی مشخص نمودن محل نقطه برش است.این کار با تولید یک عدد تصادفی بین عدد ۱ تا طول کروموزوم -۱ انجام می شود.در مثال ما عدد تصادفی باید بین ۱ تا ۳ باشد.بعد از اینکه نقطه برش را بدست آوردیم کروموزوم های والد در آن نقطه برش خورده و ژن های آنها تعویض می شود و یک فرزند جدید تولید می شود.برای مثال ما سه عدد تصادفی ذیل را تولید نمودیم

C[1] = 1,C[2] = 1,C[3] = 2

و کروموزم ها  به صورت زیر تحت تاثیر عملگر برش قرار می گیرند.همانگونه که ملاحظه می شود ژنهای والدین به ترتیب در ژن های شماره ۱، شماره ۱ و شماره ۲ برش داده می شوند.

Chromosome[1] = Chromosome[1] >< Chromosome[4]

= [02;21;18;03] >< [20;05;17;01]
= [02;05;17;01]
Chromosome[4] = Chromosome[4] >< Chromosome[5]
= [20;05;17;01] >< [10;04;13;14]
= [20;04;13;14]
Chromosome[5] = Chromosome[5] >< Chromosome[1]
= [10;04;13;14] >< [02;21;18;03]
= [10;04;18;03]

بعد از انجام اولین فرآیند برش در الگوریتم ژنتیک مورد نظرمان جمعین ما به صورت زیر خواهد بود:

Chromosome[1] = [02;05;17;01]
Chromosome[2] = [10;04;13;14]
Chromosome[3] = [12;05;23;08]
Chromosome[4] = [20;04;13;14]
Chromosome[5] = [10;04;18;03]
Chromosome[6] = [20;01;10;06]

مرحله ۵  جهش
تعداد کروموزوم هایی که جمعیت مورد جهش قرار می گیرند توسط پارامتر نرخ جهش مشخص می شوند.فرآیند جهش با تعویض تصادفی مقدار یک ژن که در یک موقعیت تصادفی قرار دارد با مقدار جدید انجام می شود.برای انجام این فرآیند مراحل که در ادامه گفته می شود را انجام می دهیم.ابتدا باید مجموع کل ژنهای موجود در جمعیت را محاسبه نماییم.که در مثال ما از فرمول زیر بدست می آید
تعداد کل ژنها=تعداد ژنهای هر کروموزوم*تعداد جمعیت =۴*۶=۲۴
فرآیند جهش با تولید یک عدد تصادفی بین ۱ و تعداد کل ژنها (۱ تا ۲۴ در مثال ما) انجام می شود.اگر مقدار عدد تصادفی تولید شده کمتر از نرخ جهش (mutaion_rate ρm) باشد در این صورت موقعیت این ژن در کروموزم نشان گذاری می شود.فرض کنیم که نرخ جهش را ۱۰٪  در نظر بگیریم ، که در این صورت انتظار داریم که ۱۰٪ ( ۰.۱) کل ژنها در جمعیت جهش داده شوند.
تعداد کل جهش ها = ۰.۱*۲۴=۲.۳≈۲
حالا اگر فرض کنیم که اعداد تصادفی که تولید شده است ۱۲ و ۱۸ باشند در این صورت کروموزم هایی که جهش دارند کروموزم شماره ۳ در ژن شماره ۴ آن و کروموزوم شماره ۵ در ژن شماره ۲ آن خواهند بود.مقدار ژنهای جهش یافته در نقطه جهش بوسیله اعداد تصادفی بین ۰ تا ۳۰ عوض می شوند.اگر اعداد تصادفی تولید شده ۲ و ۵ باشند سپس ترکیب کروموزوم ها بعد از جهش به صورت زیر است :

Chromosome[1] = [02;05;17;01]

Chromosome[2] = [10;04;13;14]
Chromosome[3] = [12;05;23;02]
Chromosome[4] = [20;04;13;14]
Chromosome[5] = [10;05;18;03]
Chromosome[6] = [20;01;10;06]

بعد از پایان فرآیند جهش یک تکرار یا یک نسل از الگوریتم ژنتیک داریم که باید این نسل جدید  را مجددا توسط تابع هدف مورد ارزیابی قرار دهیم که ارزیابی آن مانند آنچه قبلا گفته شد انجام می شود :

Chromosome[1] = [02;05;17;01]
F_obj[1] = Abs(( 02 + 2*05 + 3*17 + 4*01 ) - 30)
= Abs((2 + 10 + 51 + 4 ) - 30)
= Abs(67 - 30)
= 37
Chromosome[2] = [10;04;13;14]
F_obj[2] = Abs(( 10 + 2*04 + 3*13 + 4*14 ) - 30)
= Abs((10 + 8 + 33 + 56 ) - 30)
= Abs(107 - 30)
= 77
Chromosome[3] = [12;05;23;02]
F_obj[3] = Abs(( 12 + 2*05 + 3*23 + 4*02 ) - 30)
= Abs((12 + 10 + 69 + 8 ) - 30)
= Abs(87 - 30)
= 47
Chromosome[4] = [20;04;13;14]
F_obj[4] = Abs(( 20 + 2*04 + 3*13 + 4*14 ) - 30)
= Abs((20 + 8 + 39 + 56 ) - 30)
= Abs(123 - 30)
= 93
Chromosome[5] = [10;05;18;03]
F_obj[5] = Abs(( 10 + 2*05 + 3*18 + 4*03 ) - 30)
= Abs((10 + 10 + 54 + 12 ) - 30)
= Abs(86 - 30)
= 56
Chromosome[6] = [20;01;10;06]
F_obj[6] = Abs(( 20 + 2*01 + 3*10 + 4*06 ) - 30)
= Abs((20 + 2 + 30 + 24 ) - 30)
= Abs(76 - 30)
= 46

همانگونه که از ارزیابی کروموزوم ها در جمعیت جدید مشاهده می شود تابع هدف کاهش یافته است که به این معناست که ما کروموزومها یا راه حل های بهتری نسبت هب کروموزومهای نسل قبل داریم.بنابراین کروموزومها برای تکرار بعدی به صورت زیر خواهد بود :

Chromosome[1] = [02;05;17;01]

Chromosome[2] = [10;04;13;14]
Chromosome[3] = [12;05;23;02]
Chromosome[4] = [20;04;13;14]
Chromosome[5] = [10;05;18;03]
Chromosome[6] = [20;01;10;06]

کروموزم های جدید تحت تاثیر فرآیند مشابهی با آنچه با نسل قبلی کرموزمها انجام شد قرار می گیرند.مثل ارزیابی ، انتخاب ، برش و جهش و در پایان هر تکرار نیز نسل جدیدی از کروموزمها برای تکرار بعدی تولید میشود.این فرآیند تا رسیدن به تعداد تکرار های از پیش تعریف شده یا بدست آمدن یک شرط ادامه می یابد.در این مثال حدودا بعد از ۵۰ نسل بهترین کروموزم بدست می آید

Chromosome = [07; 05; 03; 01]

که بدان معناست که a=7,b=5,c=3,d=1 که اگر این اعداد را در معادله این که در ابتدا داشتیم قرار دهیم خواهیم داشت

a +2 b +3 c +4 d = 30

7 + (2 * 5) + (3 * 3) + (4 * 1) = 30

در این مثال ساده به خوبی کارایی و قدرت الگوریتم ژنتیک در حل مسائل بهینه سازی مشاهده می شود.

منبع : Genetic Algorithm for Solving Simple Mathematical Equality Problem

چرا منطق فازی - مجموعه های فازی

چرا منطق فازی
منطق فازی به سیستم های کامپیوتری کمک می کند تا مانند یک انسان تصمیم بگیرند و استنتاج نمایند.برای مثال هنگامی که یک دستور العمل آشپزی را دنبال می کنیم در واقع از نوعی استنتاج انسانی بهره می گیریم .مثلا سرآشپز می گوید کمی نمک این اصطلاح برای انسان ها آشناست و قابل درک اما برای کامپیوتر ها نه.منطق فازی به کمک ما می آیند تا قسمتی از استنتاج انسانی  را برای سیستم های هوش مصنوعی فراهم سازد.با یک مثال این مورد را توضیح می دهم.در خصوص اندازه گیری هوش مصنوعی با سه گروه روبه رو هستیم باهوش ، حد متوسط و کودن در واقع با سه مجموعه سر و کار داریم پس طبق تعریف مجموعه های کلاسیک هر شخص عضو یکی از این مجموعه هاست و اگر عضو  یکی بود نمی تواند عضو مجموعه دیگری باشد. سه مجموعه را به صورت زیر تعریف می کنیم :
کودن={۷۰ ،۷۱ …..۷۹}
حد متوسط = {۸۰ ،۸۱ ،…..۱۰۹}
باهوش= {۱۱۱،۱۱۰، …...،۱۳۰}

که نحوه نمایش گرافیکی این مجموعه های کلاسیک (CRISP SET ) به صورت زیر است.

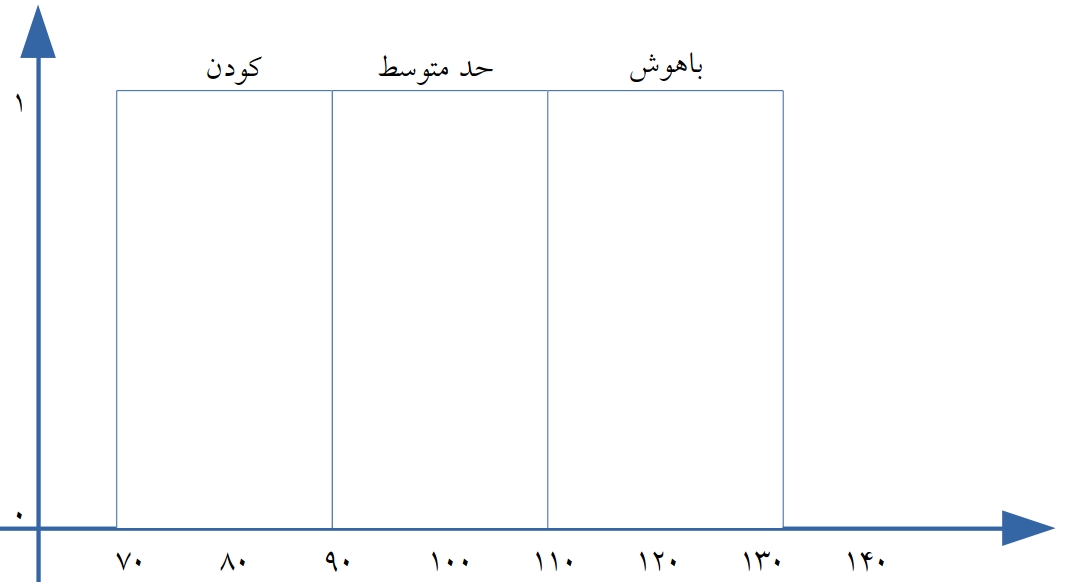
به شکل توجه کنید که درجه عضویت هر عنصر از یک مجموعه ۰ یا ۱ است.بر این اساس هوشمندی یک شخص را می توان با نسبت دادن آنها بر اساس نمره IQ که به دست آورده اند به یکی از این مجموعه ها بدست آورد.فقط یکی از مجموعه ها.حالا حالتی را در نظر می گیریم که شخص نمره تست هوش برابر ۱۰۹ دارد.مسلما هوش او بالاتر از هوش افراد حد متوسط است و شاید حتی بتوان او را جز افراد باهوش در نظر گرفت زیرا هوش او از شخصی که درای نمره هوش ۹۲ است بسیار بیشتر است اگرچه با استفاده از مجموعه  های کلاسیک این دور هر دو در یک رده هوشی قرار خواهند داشت.حالا فرض کنیم شخصی دارای نمره هوشی ۷۹ و دیگری نمره ۸۰ است مسلم است که مقایسه این دو و به این نتیجه رسید که یکی باهوش و دیگری کودن است نیز عقلانی به نظر نمی رسد و این همان نقطه است که مجموعه های کلاسیک از درک آن عاجز هستند و نقطه سقوط آنهاست.مجموعه های فازی به عناصر اجازه می دهند که یک درجه اهمیت به آنها نسبت داده شود  و مرزهای فازی با استفاده از توابع عضویت (membership function ) تعریف شوند. یک مجموعه فازی بوسیله تابع عضویت آن تعریف می شود.این توابع می توانند هر شکل دلخواهی داشته باشند اما معمولا پرکاربردترین آنها مثلثی و ذوذنقه ای هستند. نکته قابل توجه در همه اشکال منطق فازی انتقال تدریجی از نواجی کاملا خارج از یک مجموعه به نواحی کاملا داخل مجموعه می باشد که در شکل ذیل که مربوط به نمایش مثلی عبارات زبانی کودن ، حد متوسط و باهوش است قابل مشاهده است که این روند یک مقدار را قادر می نماید تا در یک مجموعه دارای عضویت بخشی ( جزیی) Partial membership باشد.در این شکل خط نقطه چین نشان دهنده چگونگی وضعیت مغزی شخص است.کسی که تست هوش وی برابر با ۱۱۵ باشد عضو دو گروه خواهد بود اما با درجه عضویت های متفاونت.همانگونه که نقطه تقاطع خط چین با مجموعه ها نشان می دهد درجه عضویت وی در مجموعه باهوش ها برابر با ۰.۷۵ و درجه عضویت وی در مجموعه حد متوسط ها برابر ۰.۲۵ است .این روش دقیقا مشاهبه عملکر استنتاج انسانی در خصوص هوشمندی افراد است.

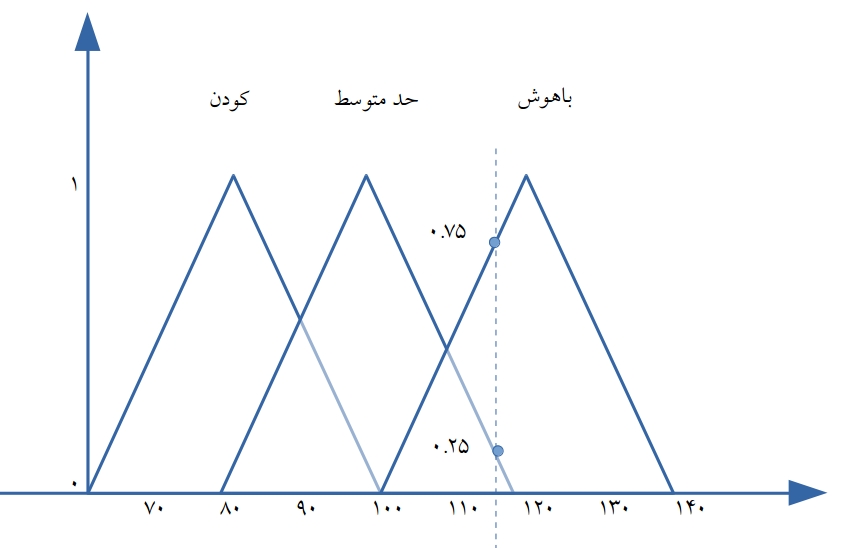
انسان این شخص را بیشتر باهوش می داند تا دارای هوش متوسط و این چیزی است که می تان از مقادیر عضویت مجموعه فازی وی می توان استنباط نمود.

معرفی منطق فازی

مقدمه :

سیستم های منطق فازی (fuzzy logic systems -fls) یک خروجی قابل قبول اما قطعی در پاسخ به یک ورودی ناقص ، مبهم ، تحریف شده و یا نادرست (fuzzy) تولید می کنند.

منطق فازی چیست ؟
منطق فازی (Fuzzy Logic -FL) یک نوع مدل  استدلال است که استدلال انسانی را شبیه سازی می کند.شیوه منطق فازی راه حل تصمیم گیری انسانی  را تقلید می‌کند به طوری که همه امکان های میانی بین مقادیری دیجیتال بله یا خیر را  در نظر گرفته و در حل مسائله درگیری می کند.
بلاک منطقی مرسوم که یک کامپیوتر آن را درک می‌کند و متوجه می‌شود یک ورودی قطعی را دریافت می‌کند و یک خروجی صریح را تولید می‌کند که این خروجی صحیح( TRUE ) یا غلط است ( FALSE). این خروجی ها شبیه  بله یا خیر انسانی هستند.مخترع منطق فازی ،پرفسور  لطفی زاده ، کشف نمود که بر خلاف کامپیوتر ها ، تصمیم های گرفته شده توسط بشر شامل یک محدوده از چیز های ممکن  در میان  بله و خیر است.از قبیل :
CERTAINLY YES -قطعا بله
POSSIBLY YES – احتمالاً بله
CANNOT SAY – نمیشه گفت
POSSIBLY NO -احتمالا نه
CERTAINLY NO – قطعاً بله

منطق فازی بر روی همه سطوح موارد(جواب های ) ممکن برای ورودی  به منظور بدست آوردن یک خروجی قطعی عمل می کند.

 پیاده‌سازی و اجرا :
سیستم منطقی فازی می‌تواند در سیستم‌هایی با اندازه ها   و محدوده توانایی متفاوت از میکرو کنترلر های کوچک تا بزرگ ، شبکه ، سیستم‌های کنترلر مبتنی بر ایستگاه کاری  پیاده‌سازی و اجرا شود.
سیستم منطق فازی می‌تواند در سخت‌افزار ها ، نرم‌افزار های و ترکیبی از هر دو پیاده‌سازی و اجرا شود.

چرا منطق فازی ؟
منطق فازی برای اهداف تجاری و علمی و کاربردی مفید است

• می‌تواند برای کنترل ماشین‌ها و محصولات مصرف کننده به کار گرفته شود
• ممکن است که استدلال دقیقی در اختیار قرار ندهد ، اما در نهایت یک استدلال قابل قبول تولید می‌کند
• منطق فازی یکی از روشها یی است که می‌تواند در محیط های غیر قطعی کاربرد داشته باشد

معماری سیستم‌های فازی :

یک سیستم منطق فازی ۴ بخش اصلی دارد که در ذیل به آن می‌پردازیم.

1- ماژول فازی سازی (Fuzzification Module)
این قسمت از سیستم منطق فازی ورودی های سیستم را که اعداد Crisp ( همان مجموعه اعداد معمولی ) را به مجموعه فازی تبدیل می کند. این ماژول سیگنال ورودی را به ۵ مرحله تقسیم می‌کند ، از جمله :
LP     x is Large Positive        X مثبت بزرگ است
MP     x is Medium Positive        X  مثبت متوسط است
S     x is Small            X کوچک است
MN     x is Medium Negative    X متوسط منفی است
LN     x is Large Negative        X بزرگ منفی است

2-پایگاه دانش : Knowledge Base

در پایگاه دانش قوانین IF-THEN هایی که توسط شخص خبره تهیه و تدوین شده‌اند قرار می گیرد.

3- موتور استنتاج (Inference Engine) :

موتور استنتاج پروسه استدلال انسانی را بوسیله ایجاد استنتاج فازی بر روی ورودی و قوانین IF-THEN شبیه سازی می‌کند

4- ماژول غیر فازی ساز (Defuzzification Module ):
ماژول غیر فازی ساز در نهایت مجموعه فازی تولید شده بوسیله موتور استنتاج را به مقداری عددی معمولی (Crisp ) تبدیل می کند.

تابع عضویت بر روی مجموعه های فازی از متغیر ها ،یکسری عملیات  را  انجام می‌دهند.
تابع عضویت :
تابع عضویت به ما اجازه می‌دهد تا که یک مجموعه فازی را به صورت گرافیکی نمایش بدهیم و موارد زبان‌شناسی مربوط به آن را تعیین کنیم.تابع عضویت برای یک مجموعه فازی مثل A بر روی متغیر universe of discourse مثل X به صورت :µA:X → [0,1] تعریف می شود.که در آن هر عنصر از X به مقداری بین ۰ و ۱ نگاشت می شود. که مقدار عضویت یا درجه عضویت نامیده می شود.که درجه عضویت عنصری در X را در مجموعه فازی A معین می کند.

• محمور X نشان دهنده  universe of discourse است.
• محور Y نشان دهنده درجه عضویت است که بین   ۰ تا ۱ متغیر است. [0,1 ].

ممکن است که چنید تابع عضویت برای فازی نمودن مقداری عددی به کار برده شود. همه توابع عضویت برای  LP, MP, S, MN و LN در شکل زیر نشان داده شده است .

تابع عضویت مثلثی شکل در میان دیگر شکل‌های تابع عضویت مثل ذوذنقه ای ، تک صفحه (singleton) و گواسین (Gaussian) عمومیت بیشتری دارند.
در این شکل ورودی برای ۵ سطح فازی کننده از -۱۰ ولت تا +۱۰ ولت متغیر است.بنابراین خروجی متناظر نیز متغیر است.

مثالی از یک سیستم منطق فازی :
اجازه بدهید تا یک سیستم تهویه هوا را با پنج سطح سیستم منطق فازی مورد بررسی قرار دهیم.این سیستم دمای سیستم تهویه هوا را با مقایسه دمای اتاق و مقدار دمای مورد نظر ( هدف) تنظیم می کند.

الگوریتم
تعریف متغیر های زبانی و شرایط ( موارد)
ساختن توابع عضویت برای آن‌ها
ساختن پایگاه داده دانش قوانین
تبدیل داده‌های معمولی (Crisp Data ) به مجموعه های داده فازی با استفاده از توابع عضویت ( فازی سازی)
ارزیابی قوانین در پایگاه قانون (موتور استنتاج)
ترکیب نتابج هر یک از قانون ها (موتور استنتاج)
تبدیل خروجی داده به مقادیر غیر فازی (غیر فازی سازی )



توسعه منطق :مرحله اول : تعریف متغیر های زبانی و شرایط ( موارد)
متغیر های زبانی ، متغیر های ورودی و خروجی در شکل کلمات ساده یا جملات هستند.برای دمای اتاق ، سرد ، گرم و غیره و غیره موارد زبانی هستند.
Temperature (t) = {very-cold, cold, warm, very-warm, hot}
هر عضوی از این مجموعه یک مورد زبانی است و می‌تواند بخشی از مقادیر دما را به طور کلی پوشش دهد.

مرحله ۲ : تولید توابع عضویت برای آن‌ها :
توابع عضویت متغیر دما در ذیل نشان داده شده است

مرحله ۳ :
ایجاغد یک ماتریکس از مقادیر دمای اتاق در مقابل مقادیر دمای هدفی که از سیستم تهویه انتظار داریم برای ما فراهم کند
دمای هدف / دمای اتاق

                                      

دمای هدف / دمای اتاق	Very_Cold	Cold	Warm	Hot	Very_Hot
Very_Cold	No_Change	Heat	Heat	Heat	Heat
Cold	Cool	No_Change	Heat	Heat	Heat
Warm	Cool	Cool	No_Change	Heat	Heat
Hot	Cool	Cool	Cool	No_Change	Heat
Very_Hot	Cool	Cool	Cool	Cool	No_Change

مجموعه قوانی را پایگاه دانش به شکل IF-THEN-ELSE تولید و ایجاد می کنیم.

Sr. No.	Condition	Action
1	IF temperature=(Cold OR Very_Cold) AND target=Warm THEN	Heat
2	IF temperature=(Hot OR Very_Hot) AND target=Warm THEN	Cool
3	IF (temperature=Warm) AND (target=Warm) THEN	No_Change

مرحله ۴ : بدست آوردن مقدار فازی
عملیات های مجموعه فازی ارزیابی قوانین را انجام می دهند. عملیات استفاده شده برای OR و AND به ترتیبی بیشینه max و کمینه MIN  می باشد.همه نتایج ارزیابی به شکل نتیجه نهایی ترکیب می شوندواین تنتیجه یک مقدار فازی است.

مرحله ۵ : انجام عملیات غیر فازی نمودن
غیر فازی نمودن انجام عملیات بر اساس تابع عضویت برای متغیر خروجی می‌باشد