تابع برازش (Finness function)

تابع برازش (Finness function) 
تعریف ساده از تابع برازش ، تابعی است که راه حل کاندید برای یک مسائله را به عنوان ورودی دریافت می‌کند و یک خروجی را که میزان خوب بودن راه حل را مشخص می‌کند ارایه می‌کند که این کار با توجه به مسائله ای که با آن سر و کار داریم در نظر گرفته می شود..محاسبه مقدار برازش (fitness) مکرراً در یک الگوریتم ژنتیک انجام می‌شود و بنابراین باید به اندازه کافی سریع باشد.محاسبه  آهسته و کند مقدار برازش(Finness) می‌تواند اثر منفی روی الگوریتم ژنتیک داشته باشد و الگوریتم را فوق‌العاده کند نماید.
در اغلب مواقع تابع برازش (fitness function) و تابع هدف(objective function) شبیه یگدیگر هستند و هر دوی آن‌ها تابع مقصود داده شده را کمینه یا پیشنه می کنند.برای مسائل پیچیده با چنید هدف و محدودیت(constraints) طراح الگوریتم ممکن است تابع های برازش مختلفی را انتخاب نماید.
تابع برازش  باید دارای ویژگی‌های زیر باشد :

• تابع برازش باید به اندازه کافی برای محاسبه سریع باشد.
• تابع برازش باید بصورت کمی چگونگی بدست آوردن راه حل مناسب یا چگونگی تولید افراد مناسب از راه حل بدست آمده را اندازه‌گیری نماید

در اغلب موارد ، محاسبه تابع برازش به دلیل پیچیدگی ذاتی مشکلی که با آن رو به رو هستیم به صورت مستقیم امکان ندارد.در  چنین مواردی از تخیمین برازش (fitness approximation) برای برآورده نمودن نیاز های خود استفاده می کنیم.
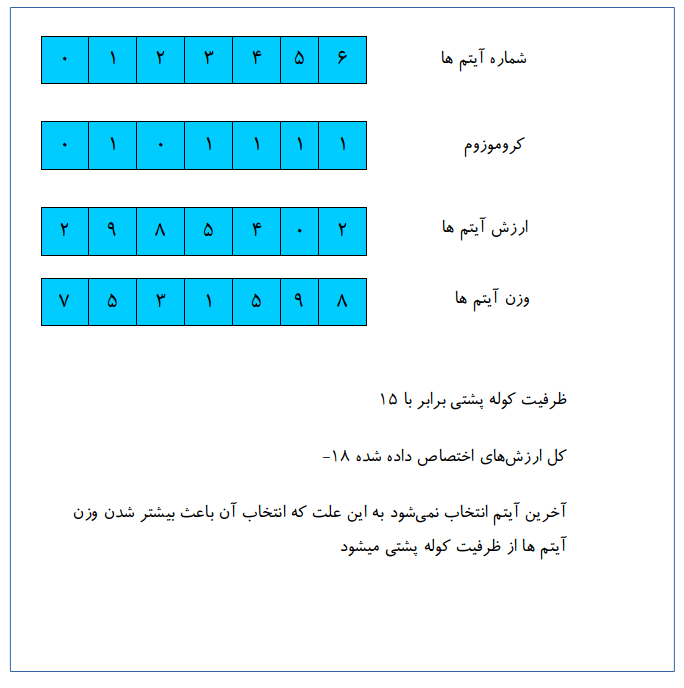
در  شکل زیر محاسبه برازش  برای مسائله کوله پشتی 0-1 نشان داده شده است.این یک تابع برازش ساده است که تنها مقادیر ارزش آیتم هایی که انتخاب شده‌اند را جمع می بندد(آنهایی که در کروموزوم با ۱ نشان داده شده اند) ، عناصر از چپ به راست اسکن می‌شوند تا زمانی که کوله پشتی پر شود.

مسائله کوله پشتی Knapsack Problem (KP)

مسائله کوله پشتی  Knapsack Problem (KP)

بر خود لازم دیدم قبل از ورود به مباحث پیشرفته تر در خصوص الگوریتم های ژنتیک و با توجه به اینکه  در مطالبی که قبلا آورده شده است و مطالب آتی مسائله کوله پشتی  به کرات مورد استفاده قرار گرفته است  ، تعریف کاملی در خصوص این مسائله برای درک بهتر خواننده داشته باشم.

مسائله کوله پشتی یک نمونه از مسائل بهینه سازی ترکیبی است (combinatorial optimization problem) که در آن بهترین راه حل از میان راه حل‌های دیگر جستجو می شود. در این مسائله یک کوله پشتی که دارای اندازه صحیح مثبت(یا ظرفیت ) است وجود دارد که این ظرفیت با V نشان داده می شود.تعداد n آیتم متفاوت که بطور بالقوه ممکن است در کوله پشتی قرار داده شوند نیز وجود دارد.آیتم I دارای یک اندازه صحیح (ظرفیت) است که با V_I  نشان داده می‌شود و  یک عدد صحیح B_I که نشان دهنده منفعت ( ارزش) این آیتم است.علاوه بر این‌ها Q_I کپی از آیتم I در دسترس می باشد.که مقدار Q_I یک عدد صحیح است که شرط زیر را مهیا نماید

1 ≤ Q _i ≤ ∞

اجازه بدهید که X_I معین نماید که چه تعداد کپی های آیتم I قرار است در کوله پشتی قرار گیرند و هدف ما به صورت زیر تعریف می‌شود که حاصل عبارت زیر را پیشینه نماییم :(قرار دادن بیشترین آیتم با بیشترین ارزش در کوله پشتی)

با این شرط که آیتم های قرار گرفته از ظرفیت کوله پشتی بیشتر نباشند :

و همچنین شرط زیر نیز صادق باشد :

1 ≤ X _i ≤ Q _i

اگر یکی یا چند تا از Q_i بی نهایت باشند ( نامتنهای) مسائله کوله پشتی را بدون کران می نامند در غیر این صورت مسائله کوله پشتی کراندار خواهد بود.مسائله کوله پشتی کراندار می‌تواند کوله پشتی 1-0 باشد ( 0-1 knapsack) و یا چند محدودیتی .اگر مقدار Q_i برابر با ۱ باشد آنگاه با یک مسائله کوله پشتی از نوع 0-1 روبه رو هستیم. در این خاص از مسائله کوله پشتی (0-1) ما نمی‌توانیم بیشتر از یک کپی از یک آیم در کوله پشتی داشته باشیم.
یک مثال برای مسائله کوله پشتی 0-1
فرض کنیم که کوله پشتی در اختیار داریم که ظرفیت آن ۱۳ اینچ مکعبت است و چندین آیتم با سایزها و ارزش‌های مختلف در ختیار داریم.می می‌خواهیم در کوله پشتی تنها آیتم هایی را داشته باشیم که در مجموع دارای یبشترین ارزش باشند با این محدودیت که مجموع ظرفیت آن‌ها از ظرفیت کوله پشتی بیشتر نشود .برای مثال ما سه آیتم وجود دارد که با حروف A,B,C برچست خورده اند.که در جدول زیر ظرفیتها (حجم) و ارزش‌های آن‌ها را مشاهده می کنید :

آیتم	A	B	C
ارزش Benefit	4	3	5
ظرفیت Volume	6	7	8

ما به دنبال این هستیم که مقدار ارزش‌های آیتم ها را بیشینه نماییم:

البته با رعایت شرایط زیر :

برای مسائله ما 2³ زیر مجموعه از آیتم ها وجود دارد که ترکیبی همگی در ذیل آورده شده است :

ارزش مجموعه	ظرفیت مجموعه	C	B	A
0	0	0	0	0
5	8	1	0	0
3	7	0	1	0
-	15	1	1	0
4	6	0	0	1
-	14	1	0	1
7	13	0	1	1
-	21	1	1	1

برای بدست آوردن بهترین راه حل مجبور هستیم که زیر مجموعه‌ای از آیتم ها که محدودیت‌های مورد نظر را دارا می‌باشند و جمع ارزش‌های آن‌ها بیشینه است را معین کنیم.در مثال ما تنها سطری که بصورت پر‌رنگ در آمده است شروط مورد نظر را فراهم می کند.بنا براین ارزش بهینه برای محدودیت مورد نظر ما ( V=13) تنها می‌تواند با یک مقدار از A ، یک مدقار از B و هیچ مقدار از C امکان‌پذیر خواهد بود که این مقدار نیز 7 بدست آمد.

جمعیت در الگوریتم های ‌ژنتیک (Population)

جمعیت در الگوریتم های ‌ژنتیک (Population).
جمعیت (Population ) زیر مجموعه‌ای از راه حل‌ها در نسل فعلی است(زایش فعلی).همچنین جمعیت را می‌توان به عنوان مجموعه‌ای از کروموزوم ها تعریف نمود.چند چیز  را هنگام کار با جمعیت در الگوریتم های ژنتیک به خاطر سپرد

• تنوع و گوناگونی جمعیت حتماً باید حفظ شود ، در غیر اینصرت موجب همگرایی زودهنگام می گردد(premature convergence).
• اندازه جمعیت نباید خیلی بزرگ باشد زیرا ممکن است که باغث کند شدن الگوریتم ژنتیک شود ، این در حالی است که جمعیت کوچکتر ممکن است که برای یک مخزن زاد و ولد(mating pool) به اندازه کافی مناسب نباشد.و این را مد نظر می‌گیریم که تصمیم برای یک جمعیت با اندازه مطلوب نیاز به آزمایش و خطا دارد.

جمعیت در الگوریتم های ژنتیک معمولاً به صورت یک آرایه دو بعدی تعریف می‌شود ( اندازه جمعیت ، اندازه x ، اندازه کروموزوم).

مقدار دهی اولیه جمعیت
دو متد اصلی برای مقدار دهی اولیه یک جمعیت در یک الگوریتم ژنتیک وجود دارد که به در زیر آورده می شوند

• مقدار دهی اولیه تصادفی (Random Initialization ) . جمعیت دارد نمودن جمعیت  اولیه با   راه حل‌های  کاملاً تصادفی
• مقدار دهی اولیه اکتشافی (ابتکاری)Heuristic initialization : جمعیت دار نمودن جمعیت اولیه با استفاده از روش‌های اکتشافی ( ابتکاری ) شناخته شده برای مسائله.

مشاهدات نشان می‌دهد که کل یک جمعیت نباید بوسیله متد اکتشافی مقداردهی اولیه شود ، زیرا ممکن است که منجر به این شود که جمعیت با راه حل‌های مشابه و تنوع بسیار کم روبه رو شویم.
به صورت تجربی مشاهده شده است که راه حل‌های تصادفی ، راه حل‌هایی هستند که جمعیت را به سمت بهینه شدن سوق می‌دهند .بنابراین با استفاده مقدار دهی اولیه اکتشافی ، تنها جمعیت با یک جفت راه حل خوب ایجاد می‌کنیم ، پس بدین منظور بقیه جمعیت را با راه حل‌های تصادفی پر می‌کنیم  به جای اینکه همه جمعیت مورد نظر خود را با راه حل‌های پر پایه اکتشاف پر نماییم.
همچنین بعضا مشاهده شده است که مقدار دهی اولیه اکتشاقی در بعضی موارد سازگاری اولیه (initial fitness) جمعیت را مورد تأثیر قرار داده است اما در پایان این تنوع در راه حل‌ها خواهد بود که منجر به بهینه سازی می شود.

مد هال جمعیت (Population Models)
دو مدل جمعیت که به صورت گسترده مورد استفاده هستند در زیر بیان می‌شود

•  حالت پایدار (Steady State) :در الگوریتم ژنتیک حالت پایدار ، در هر تکرار یک یا دو اولاد تولید می نماییم و آن‌ها یک یا پو شخص از جمعیت را جایگزین می نمایند.الگوریتم ژنتیک حالت پایدار به الگوریتم ژنتیک افزایشی (Incremental ) نیز مشهور است.
• نسل (Generational): در مدل نسل ، n اولاد تولید می‌کنیم ، که در اینجا n اندازه جمعیت می‌باشد و همه جمعیت توسط نسل جدیدتر در پایان تکرار تعویض می گردد.